2011 : WHAT SCIENTIFIC CONCEPT WOULD IMPROVE EVERYBODY'S COGNITIVE TOOLKIT?

A zero-sum game is an interaction in which one party's gain equals the other party's loss — the sum of their gains and losses is zero. (More accurately, it is constant across all combinations of their courses of action.) Sports matches are quintessential examples of zero-sum games: winning isn't everything, it's the only thing, and nice guys finish last. A nonzero-sum game is an interaction in which some combinations of actions provide a net gain (positive-sum) or loss (negative sum) to the two of them. The trading of surpluses, as when herders and farmers exchange wool and milk for grain and fruit, is a quintessential example, as is the trading of favors, as when people take turns baby-sitting each others' children.

In a zero-sum game, a rational actor seeking the greatest gain for himself or herself will necessarily be seeking the maximum loss for the other actor. In a positive-sum game, a rational, self-interested actor may benefit the other guy with the same choice that benefits himself or herself. More colloquially, positive-sum games are called win-win situations, and are capture in the cliché "Everybody wins."

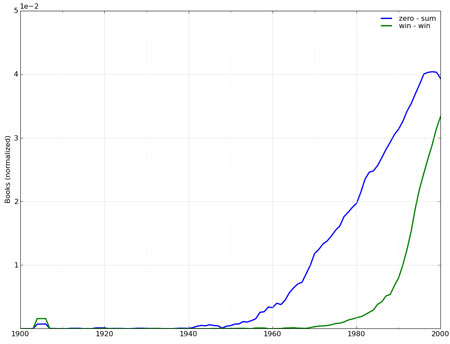
This family of concepts (zero-sum, nonzero-sum, positive-sum, negative-sum, constant-sum, and variable-sum games) was introduced by John von Neumann and Oskar Morgenstern when they invented the mathematical theory of games in 1944. The Google Books Ngram tool shows that the terms saw a steady increase in popularity beginning in the 1950s, and its colloquial relative "win-win" began a similar ascent in the 1970s.

[click to enlarge]

Once people are thrown together in an interaction, their choices don't determine whether they are in a zero- or nonzero-sum game; the game is a part of the world they live in. But people, by neglecting some of the options on the table, may perceive that they are in a zero-sum game when in fact they are in a nonzero-sum game. Moreover, they can change the world to make their interaction nonzero-sum. For these reasons, when people become consciously aware of the game-theoretic structure of their interaction (that is, whether it is positive-, negative-, or zero-sum), they can make choices that bring them valuable outcomes — like safety, harmony, and prosperity — without their having to become more virtuous, noble, or pure.

Some examples. Squabbling colleagues or relatives agree to swallow their pride, take their losses, or lump it to enjoy the resulting comity rather than absorbing the costs of continuous bickering in hopes of prevailing in a battle of wills. Two parties in a negotiation split the difference in their initial bargaining positions to "get to yes." A divorcing couple realizes that they can reframe their negotiations from each trying to get the better of the other while enriching their lawyers to trying to keep as much money for the two of them and out of the billable hours of Dewey, Cheatham, and Howe as possible. Populaces recognize that economic middlemen (particularly ethnic minorities who specialize in that niche such as Jews, Armenians, overseas Chinese, and expatriate Indians) are not social parasites whose prosperity comes at the expense of their hosts but positive-sum-game-creators who enrich everyone at once. Countries recognize that international trade doesn't benefit their trading partner to their own detriment but benefits them both, and turn away from beggar-thy-neighbor protectionism to open economies which (as classical economists noted) make everyone richer and which (as political scientists have recently shown) discourage war and genocide. Warring countries lay down their arms and split the peace dividend rather than pursuing Pyrrhic victories.

Granted, some human interactions really are zero-sum — competition for mates is a biologically salient example. And even in positive-sum games a party may pursue an individual advantage at the expense of joint welfare. But a full realization of the risks and costs of the game-theoretic structure of an interaction (particularly if it is repeated, so that the temptation to pursue an advantage in one round may be penalized when roles reverse in the next) can militate against various forms of short-sighted exploitation.

Has an increasing awareness of the zero- or nonzero-sumness of interactions in the decades since 1950 (whether referred to in those terms or not) actually led to increased peace and prosperity in the world? It's not implausible. International trade and membership in international organizations has soared in the decades that game-theoretic thinking has infiltrated popular discourse. And perhaps not coincidentally, the developed world has seen both spectacular economic growth and a historically unprecedented decline in several forms of institutionalized violence, such as war between great powers, war between wealthy states, genocides, and deadly ethnic riots. Since the 1990s these gifts have started to accrue to the developing world as well, in part because they have switched their foundational ideologies from ones that glorify zero-sum class and national struggle to ones that glorify positive-sum market cooperation. (All these claims can be documented from the literature in international studies.)

The enriching and pacifying effects of participation in positive-sum games long antedate the contemporary awareness of the concept. The biologists John Maynard Smith and Eörs Szathmáry have argued that an evolutionary dynamic which creates positive-sum games drove the major transitions in the history of life: the emergence of genes, chromosomes, bacteria, cells with nuclei, organisms, sexually reproducing organisms, and animal societies. In each transition, biological agents entered into larger wholes in which they specialized, exchanged benefits, and developed safeguards to prevent one from exploiting the rest to the detriment of the whole. The journalist Robert Wright sketched a similar arc in his book Nonzero and extended it to the deep history of human societies. An explicit recognition among literate people of the shorthand abstraction "positive-sum game" and its relatives may be extending a process in the world of human choices that has been operating in the natural world for billions of years.